a) Esfuerzo y deformacion.
El ensayo de traccion es uno de los mas importantes para determinar las propiedades mecanicas de los materiales.
El ensayo consiste en someter una pieza de forma cilindrica o prismatica de
dimensiones normalizadas (estandar) a un esfuerzo de traccion continuo (tendencia a
estirar el material). Esta pieza se llama probeta:
Consideremos una probeta de longitud lo y una seccion Ao sometida a una fuerza F norma de traccion
(perpendicular a la seccion de la probeta).
Se define esfuerzo o tension(σ) como la fuerza aplicada a la probeta por unidad de seccion transversal Ao
σ= F/Ao
Sus unidades en el Sistema Internacional son
N / m2 = pascal
Supongamos que durante el ensayo la varilla se alargo una longitud l
Δl = l – lo
siendo l = longitud final de la probeta
y lo = longitud inicial de la probeta
Definimos deformacion o alargamiento unitario (ε) de la probeta como el cociente entre el cambio de longitud o alargamiento experimentado y su longitud inicial.
ε= (l−lo) / lo = = Δl / lo ----> No tiene unidades
A veces se utiliza el porcentaje de alargamiento.
% deformacion = ε (%) = Δl / lo ⋅100
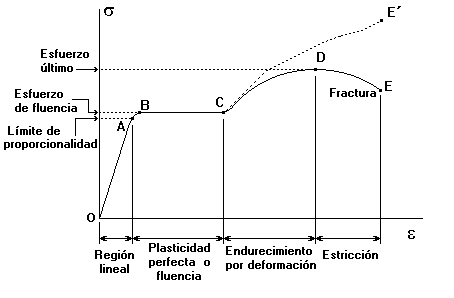
Análisis de un diagrama de deformación
Supongamos una probeta sometida a tracción cuyos resultados se representan en una gráfica: En abscisas la elongación o alargamiento ( Δl) y en ordenadas la fuerza aplicada (F) que provoca la deformacion.
Cada material tiene una grafica distinta porque su comportamiento es distinto.
En general hay dos zonas
· En la primera la deformacion es proporcional a la tension de traccion.
· En la segunda, a pequenas variaciones de tension se producen grandes
deformaciones.
Esta informacion es util, pero no es practica y se utilizan otras magnitudes.
En abscisas, la deformacion es ε = Δl / lo
En ordenadas, al tension o esfuerzo σ= F/ Ao (siendo Ao la seccion de la probeta en cm2 y σ la tension en la seccion transversal en kp/cm2)
Un material presenta dos zonas en cuanto a su comportamiento ante un
esfuerzo de traccion:
1. Zona elastica (OE): Se caracteriza porque al cesar las tensiones aplicadas, los materiales recuperan su longitud inicial (lo)
2. Zona plastica (ES): Se ha rebasado la tension del limite elastico y, aunque dejemos de aplicar tensiones de σε traccion, el material ya no recupera su su longitud original y será mayor que lo
En la zona elastica (OE) hay, a su vez, dos zonas:
Puedes visitar este enlace para ver la relación entre la gráfica y el ensayo:
http://www.youtube.com/watch?v=ktAi5jiyvPg&feature=player_embedded-Zona de proporcionalidad (OP): En la grafica es una linea recta , es decir, el alargamiento unitario (ε) es proporcional a la tension ejercida (σ).
σ = constante ・ ε
La constante se representa por la letra E y se llama modulo de elasticidad longitudinal o modulo de Young. En el sistema internacional, sus unidades son N / m2
-Zona no proporcional (PE): El material se comporta de forma elastica, pero no existe una relacion proporcional entre tension y deformacion. En la zona plastica (BE) hay, a su vez, otras dos zonas:
a) Zona de deformacion plastica uniforme o zona de limite de rotura (ER): Se consiguen grandes alargamientos con un pequeno incremento de la tension. En el punto R existe el limite de rotura y la tension en ese punto se llama tension de rotura ( σ R). A partir de este punto, la probeta se considera rota, aunque fisicamente no lo este.
En este enlace se ve fácilmente.
http://www.steeluniversity.org/content/html/spa/default.asp?catid=150&pageid=2081271532b) Zona de rotura o zona de estriccion o zona de deformacion plastica localizada (RS): Las deformaciones son localizadas y, aunque disminuya la tension, el material se deforma hasta la rotura. En el punto D, la probeta se ha fracturado. La seccion de la probeta se reduce drasticamente.
Esta curva varia de un material a otro, e incluso, otros materiales presentan curvas distintas (acero).
En el acero existe una zona por encima del limite elastico en el que se da una deformacion apreciable sin que varie la tension aplicada. Este fenomeno es la fluencia y el punto donde comienza a manifestarse el fenomeno es la tension de fluencia. Zona (EF).
Una vez definida la curva de traccion, veamos algunas definiciones:
a) Limite de elasticidad o limite elastico (σE): La tension a partir de la cual las deformaciones dejan de ser reversibles, es decir, la probeta no recuperara su forma inicial.
b) Limite de rotura o tension de rotura (σR): Maximo valor de la tension observable
en un diagrama tension-deformacion. Esta es la maxima tension que soporta la
probeta.
c) Modulo de Young (E): Constante que representa la relacion entre la tension y la deformacion en la zona proporcional. Tambien se le llama modulo de elasticidad.
d) Limite de proporcionalidad (σP): La tension a partir de la cual deja de cumplirse la relacion proporcional entre tension y deformacion y, por lo tanto, se deja de cumplir la ley de Hooke.
e) Limite de fluencia (σF): valor de la tension que soporta la probeta en el momento de producirse el fenomeno de la fluencia.
f) Estriccion: es la reduccion de la seccion que se produce en la zona de la rotura Curvas para un material ductil y de poca resistencia y otro de alta resistencia , pero fragil:
b) La ley de Hooke
Se aplica en ensayos de traccion y con caracter general se enuncia asi:
“Las deformaciones producidas en un elemento resistente son proporcionales a las fuerzas que lo producen”.
Fuerza / Deformacion =constante= tg α
La fuerza es de traccion (F) y la deformacion Δl = l – lo
La constante se representa por K = tg α

Unidades:
F = En el sistema internacional Newton (N), tambien se elige kilopondio (Kp)
Δl = En el sistema internacional Metros (m), tambien se elige cm o mm
K en el Sistema Internacional N/m , tambien se elige Kp/cm o Kp/mm
c) Tension maxima de trabajo
Cuando se diseña un elemento de una estructura es preciso conocer todas las fuerzas que se ejercen sobre él, para calcular su sección de tal forma que se encuentre dentro de la zona de proporcionalidad entre deformación y tensión. De este modo se asegura que la deformación sufrida por el material sea reversible y proporcional a la tensión soportada. Se representa por (σt)
Hasta que la tension no alcanza (σt) podemos asegurar...
a) Que el elemento no padecera deformaciones plasticas
b) Que cumplira la ley de Hooke
c) Que ofrecera un margen de seguridad ante la posibilidad de que aparezcan fuerzas
imprevistas.
No hay comentarios:
Publicar un comentario